1713: The Bernoulli Distribution and Probability Theory

Author David Poole on 9 December 2017 David Poole's blog

Formulated by Jacob Bernoulli from Basel, the Bernoulli Distribution describes events having exactly two outcomes e.g. if a flipped coin will come up heads or not, if a rolled dice will be a 6 or another number, or whether you do or do not click the “Read more” link in this post!

More formally, it is the probability distribution of a random variable taking on only two values, “success” and “failure” with respective probabilities pand 1 – p. Each trial is referred to as a Bernoulli Trial. A key point is that each event resulting from a Bernoulli Trial must be completely independent of the previous event.

The Bernoulli distribution is the probability distribution of a random variable  having the probability density function.

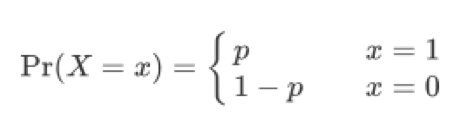
for 0 < p < 1.

Intuitively, it describes a single experiment having two outcomes: success (“1”) occurring with probability pand failure (“0”) occurring with probability 1 – p. 

A closed form of the probability density function of Bernoulli distribution is

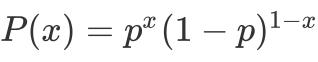
The importance of independence

An important part of every Bernoulli trial is that each action must be independent, which means that each event must be completely separate and have nothing to do with the previous event.  For example: If two cards are drawn with replacement from a deck of cards, the event of drawing a red card on the first trial and that of drawing a red card on the second trial are independent. By contrast, if two cards are drawn without replacement from a deck of cards, the event of drawing a red card on the first trial and that of drawing a red card on the second trial are not independent, because a deck that has had a red card removed has proportionately fewer red cards.

The Bernouilli process leads to several probability distributions: 

• The binomial distribution
• The geometric distribution
• The negative binomial distribution

Ars Conjectandi – the art of conjecturing

Jacob Bernoulli’s most original work was Ars Conjectandi published in Basel in 1713, eight years after his death. It is considered a work of the greatest significance in the theory of probability. By the “art of conjecturing” Bernoulli meant an approach by which one could choose more appropriate, safer, more carefully considered, and more probable actions in matters in which complete certainty is impossible. He believed that his proof of a new fundamental theorem – later called the Weak Law of Large Numbers – showed that the mathematics of games of chance could be extended to a wide range civil, moral, and economic problems. 

The Weak Law of Large Numbers, also known as Bernoulli’s theorem, states that if you have a sample of independent and identically distributed random variables, as the sample size grows larger, the sample mean will tend toward the population mean.

About Jacob Bernoulli, b. 1655, d. 1705, Basel

One of the famous Bernoulli family of mathematicians, Jacob Bernoulli was born inBasel, Switzerland in 1655 and taught mechanics at the University in Basel from 1683. Although he died at the relatively young age of 50 in 1705, his enormous contribution to the field of probability lives on.

References and further reading

1. https://brilliant.org/wiki/bernoulli-distribution/
2. https://en.wikipedia.org/wiki/Jacob_Bernoulli
3. https://www.statistics.gov.hk/wsc/IPS008-P1-S.pdf
4. https://medium.com/human-in-a-machine-world/weak-law-of-large-numbers-270968e28c3b
5. https://en.wikipedia.org/wiki/Probability_density_function
6. Ars Conjectandi: https://en.wikipedia.org/wiki/Ars_Conjectandi
7. Independence: https://en.wikipedia.org/wiki/Independence_(probability_theory)#Drawing_cards